Using Calculus To Derive The Freefall Formula

The Position Equation (also known as the freefall formula)  S = -16t²  + V_ot + S_o is often cited in college algebra textbooks. In this formula, S represents the height (in feet) of an object thrown into the air at any time t (in seconds) where V_o is the velocity at which the object is thrown upward (or downward) and S_o is the height of the object when it is thrown. Also, this equation only works with the acceleration of gravity on the surface of the earth of 32 feet per second each second. The equation for any gravity and units is S = at²  + V_ot + S_o.

Where Does This Formula Come From?

This is not some formula a physics or math professor made up out of the blue, centuries ago. Rather, this is a formula that is a direct result of integrating the acceleration function representing gravity.  From calculus, we can write acceleration as a =  s''(t) where s''(t) is the second derivative of distance with respect to time (i.e. the rate of the change in velocity with respect to time) and a=-32 ft/sec2 represents the acceleration due to gravity.

Integrate both sides of s''(t) = -32 with respect to t to get

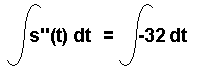
This results in s'(t) = -32t + C₁ where C₁ is a constant and s'(t) is the velocity at any time t.

At time t=0, s'(t) is equal to the initial velocity V_o so we get C₁ = V_o. The new equation is

s'(t) = -32t + V_o

Now, integrate both sides with respect to t to get

This results in

where C₂ is a constant and s(t) is the position at any time t.

At time t=0, s(t) is equal to the initial position S_o so we get C₂ = S_o. The final equation is

  or simplified 

Does none of this make sense? With successful completion of Calculus I & II this would make complete sense. Furthermore, you can not really understand physics unless you fully understand how the formulas are derived.

Remember: Physics = Mathematics Applied To The World Around Us