Properties of Rational Functions

RF1 -  Definition of a Reduced Rational Function: If f(x) consists of a ratio of two polynomials P(x) and Q(x) where the degree of Q(x) is at least 1, then f(x) is a Rational Function.

If P(x) and Q(x) contain no identical factors, the f(x) is a Reduced Rational Function.

RF2 -  Vertical Asymptotes: The vertical asymptotes of a rational function in reduced form consist of vertical lines of the form x=a where "a" is any value of x resulting in division by zero.

As x-values of the rational function approach the vertical asymptote value x=a from the right or the left, the y-value of the function will increase to infinity or decrease to negative infinity.

RF3 -  Horizontal Asymptotes: The horizontal asymptote of a rational function in reduced or unreduced form consists of a horizontal line of the form y=b where "b" is the value of f(x) as x approaches positive or negative infinity.

For rational functions where the degree of the denominator is greater than the degree of the numerator, y = 0 will be the horizontal asymptote.

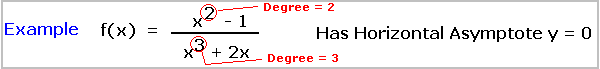
For rational functions of the form where m=n

y = a_m/b_n will be horizontal asymptote. In other words, if the degrees of numerator and denominator are equal, then the horizontal asymptote will consist of the horizontal line equal to the ratio of the leading coefficients.

RF4 -  Slant Asymptotes: The slant asymptote of a rational function consists of a slanted line of the standard linear form y=mx + b, m≠0, where the graph of f(x) approaches this linear function as x approaches positive or negative infinity.

The slant asymptote only occurs if the numerator is of degree one more than the degree of the denominator.  The slant asymptote may be found by dividing the numerator of the rational function by the denominator and rewriting the rational function as this result.  The slant asymptote will be equal to the non-fractional part of this result.

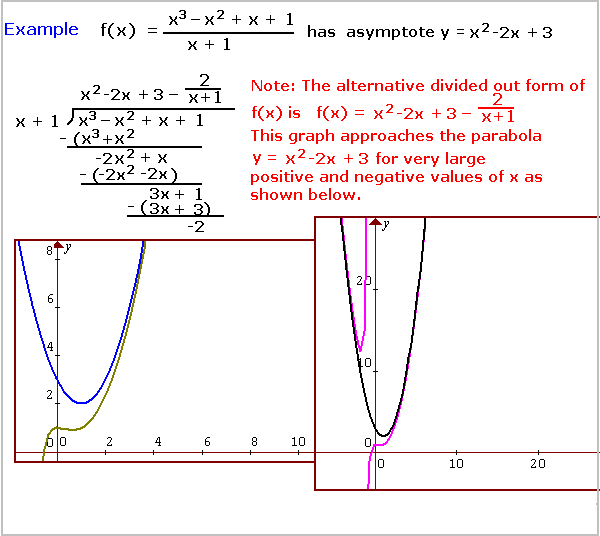
RF5 -  Higher Degree Asymptotes:

If the degree of the numerator is two or more greater than the degree of the denominator, then there will be an asymptote of degree equal to the difference in degrees.  This higher degree asymptote may be found by dividing the numerator of the rational function by the denominator and rewriting the rational function as this result.  The higher degree asymptote will be equal to the non-fractional part of this result.