How Albert Einstein Started His Career in Physics and Mathematics

In 1889, a family friend named Max Talmud (later: Talmey), a medical student, introduced the ten-year-old Albert to key science and philosophy texts, including Kant's Critique of Pure Reason and Euclid's Elements (Einstein called it the "holy little geometry book") From Euclid, Albert began to understand deductive reasoning (integral to theoretical physics), and by the age of twelve, he learned Euclidean geometry from a school booklet. He soon began to investigate calculus.¹ From http://en.wikipedia.org/wiki/Albert_Einstein#_note-HarvChemAE

What are Euclid's Elements About?

Euclid's Elements is a mathematical work made up of 13 books written by the Greek mathematician Euclid in circa 300BC. Each book contains definitions, postulates (self-evident truths), propositions, and theorems in the study of Geometry and Number Theory. The Elements make up the oldest formal and deductive treatment of mathematics. Reproducing the proofs of some of the propositions have been an integral tool in training one's mind to think in a logical and deductive manner from Euclid's time to the present.

An Example of a Deductive Proof From Euclid's Elements - Book I, Proposition 6

If in a triangle two angles equal one another, then the sides opposite the equal angles also equal one another.

The The way to prove this is to assume that the conclusion is false the sides opposite the equal angles do not equal one another. while assuming that the premise in a triangle two angles equal one another is true and show that there is a contradiction. In this way, we indirectly prove that the original if-then statement is true.  This method of proof, known as Reductio ad Absurdum  (or proof by contradiction) is widely used in higher mathematics and science.

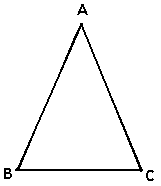
Given a triangle ABC as shown below We are assuming that angle ABC is equal to angle ACB yet sides AB and AC are not equal.	Justification This is our assumption
Since AB does not equal AC, then one side must be greater. We let AB be greater.	This is a Common Notion of Euclid's Elements.
We can construct a triangle DBC where sides DB = AC.	This is justified by Postulate 1 of Book 1 and Proposition 3 of Book 1 which states that if two segments are unequal, the longer may be "cut off" to the length of the shorter.
We can now say that triangle ACB is equal to triangle DBC since these triangles have a corresponding side, angle, and a side that  are equal.	This is justified by Proposition 4 of Book 1 which is commonly known in Geometry as the Side-Angle-Side Theorem.
Since DB is constructed by cutting off AB, DC < AB and also DB < AB by our original assumption.	This is justified by a Common Notion that states "the whole is greater than the part".
We have equated a smaller triangle to a larger triangle, which is a contradiction. This contradiction proves If in a triangle two angles equal one another, then the sides opposite the equal angles also equal one another.	Proof by contradiction.

This proof is a rewording of a proof give at http://aleph0.clarku.edu/~djoyce/java/elements/bookI/propI6.html.

Are These Methods Still Taught In Schools Today?

Yes, Euclid's methods of proof, so valued by Albert Einstein and countless scientists and mathematicians are still taught in high school geometry courses. An example of a 2-column proof is given here and a discussion of high school geometry proofs is given here.

¹  Dudley Herschbach, "Einstein as a Student," Department of Chemistry and Chemical Biology, Harvard University, Cambridge, MA, USA, page 3, web: HarvardChem-Einstein-PDF: about Max Talmud visited on Thursdays for 6 years.